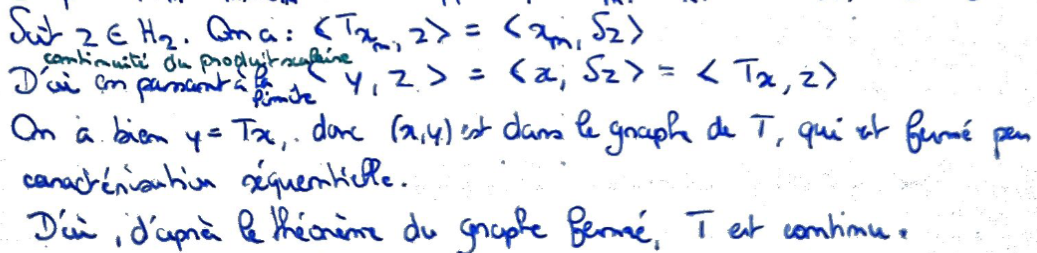Démonstration du théorème du graphe fermé.

Sens \((i)\implies(ii)\).

Le graphe est l'image réciproque de \(\{0\}\) par une fonction continue.

Démonstration du théorème du graphe fermé.

Sens \((i)\impliedby(ii)\).

On munit \(E\times F\) de la norme constituée de la somme des normes. Cet espace est alors complet.

En particulier, le graphe est complet en tant que fermé d'un complet.

La projection sur \(E\) est ainsi linéaire, continue et bijective.

Par Théorème d'isomorphisme de Banach, la réciproque est continue, ce qui donne la continuité de \(L\).

Soient \((H_1,\langle{\cdot,\cdot}\rangle _1)\) et \((H_2,\langle{\cdot,\cdot}\rangle _2)\) deux espaces de Hilbert et \(T:H_1\to H_2\) une application linéaire.
On suppose qu'il existe une application linéaire \(S:H_2\to H_1\) tq $$\forall x\in H_1,\forall y\in H_2,\quad\langle{Tx,y}\rangle _2=\langle{x,Sy}\rangle _1.$$
Montrer que \(T\) et \(S\) sont continues.

On va utiliser le Théorème du graphe fermé.

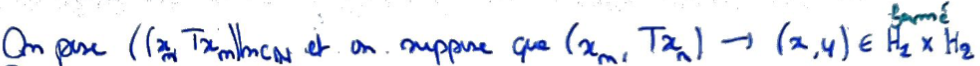
On conclut en utilisant les données de l'énoncé et par continuité du produit scalaire.

Soit \(F\) un sous-espace vectoriel Fermé de \(\mathcal C([0,1])\) muni de la norme de la convergence uniforme.
On suppose que tous les éléments de \(F\) sont dans \(\mathcal C^1([0,1])\).
En utilisant le Théorème du graphe fermé, montrer qu'il existe \(C\gt 0\) tq $$\forall f\in F,\quad\lVert f^\prime\rVert_\infty\leqslant C\lVert f\rVert_\infty.$$

On pose la fonction de dérivation \(\to\) on veut montrer qu'elle est continue.

On a bien la continuité via Théorème fondamental d'analyse et inversion limite/intégrale pour la convergence uniforme.

Puisque \(T\) est linéaire, on a la conclusion.